Posted Updated 算法 / 栈与队列21 minutes read (About 3125 words)

栈与队列

栈与队列是常用的数据结构，其中栈提供先进后出，队列提供先进先出，这样的数据结构可以解决一些需要顺序解决的问题。在java中实现底层是不一样的原因是栈是以底层容器完成其所有的工作，对外提供统一的接口，底层容器是可插拔的（也就是说我们可以控制使用哪种容器来实现栈的功能）。

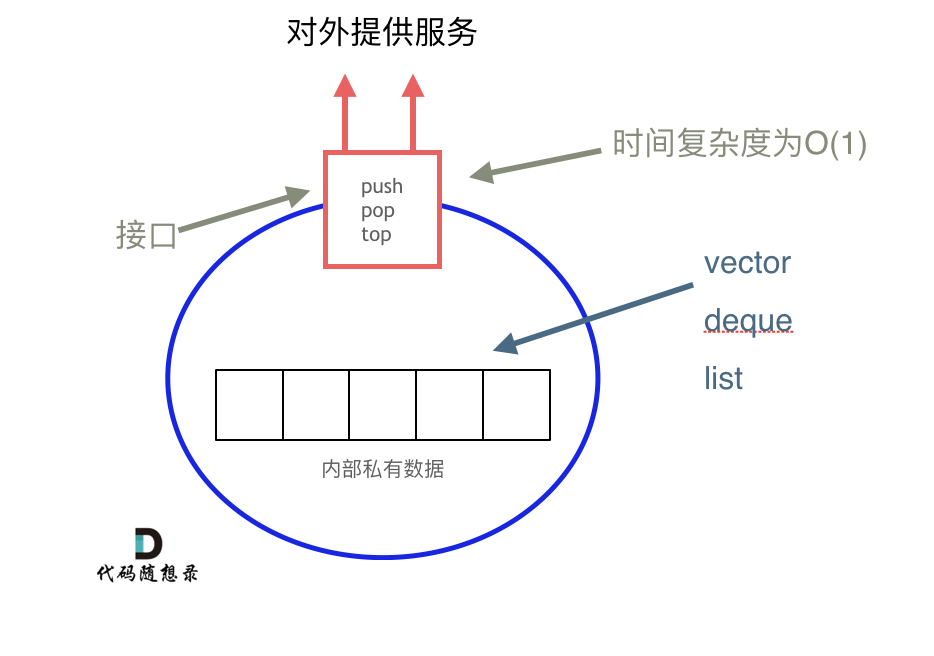
在Java中，队列和栈是两种常见的数据结构，它们分别用于不同的场景，而它们的实现通常基于以下几种容器：

队列（Queue）的容器实现：

  1. LinkedList：

    • java.util.LinkedList 是一个双向链表，支持在两端进行元素的添加和删除，因此适用于实现队列。
    • 可以使用 offer() 在队尾添加元素，使用 poll() 移除并返回队头元素。
    1
    2
    3
    4
    Queue<Integer> queue = new LinkedList<>();
    queue.offer(1);
    queue.offer(2);
    int frontElement = queue.poll();

  2. ArrayDeque：

    • java.util.ArrayDeque 是一个基于数组的双端队列，同样适用于实现队列。
    • 可以使用 offer() 在队尾添加元素，使用 poll() 移除并返回队头元素。
    1
    2
    3
    4
    Queue<Integer> queue = new ArrayDeque<>();
    queue.offer(1);
    queue.offer(2);
    int frontElement = queue.poll();

  3. PriorityQueue：

    • java.util.PriorityQueue 是一个基于优先级堆的无界优先级队列，可以实现具有优先级的队列。
    • 元素按照优先级顺序被移除。
    1
    2
    3
    4
    Queue<Integer> priorityQueue = new PriorityQueue<>();
    priorityQueue.offer(3);
    priorityQueue.offer(1);
    int highestPriority = priorityQueue.poll();

栈（Stack）的容器实现：

  1. LinkedList：

    • java.util.LinkedList 可以用作栈的实现，因为它是一个双向链表，支持在两端进行元素的添加和删除。
    • 可以使用 push() 入栈，pop() 出栈，peek() 查看栈顶元素。
    1
    2
    3
    4
    Deque<Integer> stack = new LinkedList<>();
    stack.push(1);
    stack.push(2);
    int topElement = stack.pop();

  2. ArrayDeque：

    • java.util.ArrayDeque 同样可以用作栈的实现，支持在两端进行元素的添加和删除。
    • 可以使用 push() 入栈，pop() 出栈，peek() 查看栈顶元素。
    1
    2
    3
    4
    Deque<Integer> stack = new ArrayDeque<>();
    stack.push(1);
    stack.push(2);
    int topElement = stack.pop();

注意：在现代Java编程中，推荐使用 Deque 接口来代替 Stack 类，因为 Deque 提供了更灵活的双端队列操作，并且 Stack 类是一个遗留类。

232.用栈实现队列

力扣题目链接

如果要用栈实现队列，那么就要保证先进先出，所以就必须用两个栈，一个负责弹出到底部一个负载接收其他变量。

1
2
3
4
5
6
7
8
9
10
11
12
stackIn = new Stack<>(); // 负责进栈
stackOut = new Stack<>(); // 负责出栈   
public int pop() {    
        dumpstackIn();
        return stackOut.pop();
    }
    private void dumpstackIn(){
        if (!stackOut.isEmpty()) return; 
        while (!stackIn.isEmpty()){
                stackOut.push(stackIn.pop());
        }
    }

225. 用队列实现栈

力扣题目链接

这个有多种实现思路，可以在放入队列时就保证出栈顺序。也可以在出队列时出最后一个，还可以使用一个队列循环size长度然后把出队的元素重新入队，直到找到最后一个元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
    /** 思路1：两个队列在放入时保证出队顺序 */
class MyStack {

    Queue<Integer> queue1; // 和栈中保持一样元素的队列
    Queue<Integer> queue2; // 辅助队列

    /** Initialize your data structure here. */
    public MyStack() {
        queue1 = new LinkedList<>();
        queue2 = new LinkedList<>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        queue2.offer(x); // 先放在辅助队列中
        while (!queue1.isEmpty()){
            queue2.offer(queue1.poll());
        }
        Queue<Integer> queueTemp;
        queueTemp = queue1;
        queue1 = queue2;
        queue2 = queueTemp; // 最后交换queue1和queue2，将元素都放到queue1中
    }
 /** 思路2：两个队列在放入时保证出队顺序 */
    // Deque 接口继承了 Queue 接口
    // 所以 Queue 中的 add、poll、peek等效于 Deque 中的 addLast、pollFirst、peekFirst     
        Deque<Integer> que1; // 和栈中保持一样元素的队列
    	Deque<Integer> que2; // 辅助队列
        public int pop() {
        int size = que1.size();
        size--;
        // 将 que1 导入 que2 ，但留下最后一个值
        while (size-- > 0) {
            que2.addLast(que1.peekFirst());
            que1.pollFirst();
        }

        int res = que1.pollFirst();
        // 将 que2 对象的引用赋给了 que1 ，此时 que1，que2 指向同一个队列
        que1 = que2;
        // 如果直接操作 que2，que1 也会受到影响，所以为 que2 分配一个新的空间
        que2 = new ArrayDeque<>();
        return res;
    }
     /** 思路3：一个队列，一边放一边添加 */
    class MyStack {
    // Deque 接口继承了 Queue 接口
    // 所以 Queue 中的 add、poll、peek等效于 Deque 中的 addLast、pollFirst、peekFirst
    Deque<Integer> que1;
        public int pop() {
        int size = que1.size();
        size--;
        // 将 que1 导入 que2 ，但留下最后一个值
        while (size-- > 0) {
            que1.addLast(que1.peekFirst());
            que1.pollFirst();
        }

        int res = que1.pollFirst();
        return res;
    }

20. 有效的括号

力扣题目链接

两种情况比较遇见左括号就入栈右括号和遇到左括号就入栈左括号对比，可以看到如果采用遇到左括号就入栈右括号就不用进行匹配了可以直接相等比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for (int i = 0; i < s.length(); i++) {
    char currentChar = s.charAt(i);

    if (currentChar == '(' || currentChar == '[' || currentChar == '{') {
        stack.push(currentChar);
    } else if (currentChar == ')' || currentChar == ']' || currentChar == '}') {
        if (stack.isEmpty() ||
                (currentChar == ')' && stack.peek() != '(') ||
                (currentChar == ']' && stack.peek() != '[') ||
                (currentChar == '}' && stack.peek() != '{')) {
            return false; // Mismatched brackets
        }
        stack.pop(); // Matching pair found, remove the opening bracket
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
    for (int i = 0; i < s.length(); i++) {
        ch = s.charAt(i);
        //碰到左括号，就把相应的右括号入栈
        if (ch == '(') {
            deque.push(')');
        }else if (ch == '{') {
            deque.push('}');
        }else if (ch == '[') {
            deque.push(']');
        } else if (deque.isEmpty() || deque.peek() != ch) {
            return false;
        }else {//如果是右括号判断是否和栈顶元素匹配
            deque.pop();
        }
    }
    //最后判断栈中元素是否匹配
    return deque.isEmpty();
}

1047. 删除字符串中的所有相邻重复项

力扣题目链接

很简单的逻辑如果，某个元素和栈顶元素一样就出栈栈顶，不一样就入栈。这里简单介绍三个方法

方法1：列表

链接结构可能是最糟糕的结构，每个元素上都有缓存未命中而进行迭代。最重要的是，它们消耗更多的内存。

如果您需要添加/删除两端，ArrayDeque 明显优于 LinkedList。对于循环队列来说，随机访问每个元素也是 O(1)。

链表唯一更好的操作是在迭代期间删除当前元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public String removeDuplicates(String S) {
        //ArrayDeque会比LinkedList在除了删除元素这一点外会快一点
        //参考：
        ArrayDeque<Character> deque = new ArrayDeque<>();
        char ch;
        for (int i = 0; i < S.length(); i++) {
            ch = S.charAt(i);
            if (deque.isEmpty() || deque.peek() != ch) {
                deque.push(ch);
            } else {
                deque.pop();
            }
        }
        String str = "";
        //剩余的元素即为不重复的元素
        while (!deque.isEmpty()) {
            str = deque.pop() + str;
        }
        return str;
    }
}

方法2双指针快指针指向需要匹配元素 ，慢指针指向已经匹配元素，其中的slow–和slow++是灵魂，slow–代表如果匹配就删除数组中的slow，slow++不匹配就向前移动。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
lass Solution {
    public String removeDuplicates(String s) {
        char[] ch = s.toCharArray();
        int fast = 0;
        int slow = 0;
        while(fast < s.length()){
            // 直接用fast指针覆盖slow指针的值
            ch[slow] = ch[fast];
            // 遇到前后相同值的，就跳过，即slow指针后退一步，下次循环就可以直接被覆盖掉了
            if(slow > 0 && ch[slow] == ch[slow - 1]){
                slow--;
            }else{
                slow++;
            }
            fast++;
        }
        return new String(ch,0,slow);
    }
}

239. 滑动窗口最大值

力扣题目链接

需要返回滑动窗口的最大值，这可以使用一个单调队列

其实队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//解法一
//自定义数组
class MyQueue {
    Deque<Integer> deque = new LinkedList<>();
    //弹出元素时，比较当前要弹出的数值是否等于队列出口的数值，如果相等则弹出
    //同时判断队列当前是否为空
    void poll(int val) {
        if (!deque.isEmpty() && val == deque.peek()) {
            deque.poll();
        }
    }
    //添加元素时，如果要添加的元素大于入口处的元素，就将入口元素弹出
    //保证队列元素单调递减
    //比如此时队列元素3,1，2将要入队，比1大，所以1弹出，此时队列：3,2
    void add(int val) {
        while (!deque.isEmpty() && val > deque.getLast()) {
            deque.removeLast();
        }
        deque.add(val);
    }
    //队列队顶元素始终为最大值
    int peek() {
        return deque.peek();
    }
}

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums.length == 1) {
            return nums;
        }
        int len = nums.length - k + 1;
        //存放结果元素的数组
        int[] res = new int[len];
        int num = 0;
        //自定义队列
        MyQueue myQueue = new MyQueue();
        //先将前k的元素放入队列
        for (int i = 0; i < k; i++) {
            myQueue.add(nums[i]);
        }
        res[num++] = myQueue.peek();
        for (int i = k; i < nums.length; i++) {
            //滑动窗口移除最前面的元素，移除是判断该元素是否放入队列
            myQueue.poll(nums[i - k]);
            //滑动窗口加入最后面的元素
            myQueue.add(nums[i]);
            //记录对应的最大值
            res[num++] = myQueue.peek();
        }
        return res;
    }
}

347.前 K 个高频元素（review）

力扣题目链接

什么是优先级队列呢？

其实就是一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。

所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素），如果懒得自己实现的话，就直接用priority_queue（优先级队列）就可以了，底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆。

所以我们要用小顶堆，因为要统计最大前k个元素，只有小顶堆每次将最小的元素弹出，最后小顶堆里积累的才是前k个最大元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/*Comparator接口说明:
 * 返回负数，形参中第一个参数排在前面；返回正数，形参中第二个参数排在前面
 * 对于队列：排在前面意味着往队头靠
 * 对于堆（使用PriorityQueue实现）：从队头到队尾按从小到大排就是最小堆（小顶堆），
 *                                从队头到队尾按从大到小排就是最大堆（大顶堆）--->队头元素相当于堆的根节点
 * */
class Solution {
    //解法1：基于大顶堆实现
    public int[] topKFrequent1(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数
        for(int num:nums){
            map.put(num,map.getOrDefault(num,0)+1);
        }
        //在优先队列中存储二元组(num,cnt),cnt表示元素值num在数组中的出现次数
        //出现次数按从队头到队尾的顺序是从大到小排,出现次数最多的在队头(相当于大顶堆)
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2)->pair2[1]-pair1[1]);
        for(Map.Entry<Integer,Integer> entry:map.entrySet()){//大顶堆需要对所有元素进行排序
            pq.add(new int[]{entry.getKey(),entry.getValue()});
        }
        int[] ans = new int[k];
        for(int i=0;i<k;i++){//依次从队头弹出k个,就是出现频率前k高的元素
            ans[i] = pq.poll()[0];
        }
        return ans;
    }
    //解法2：基于小顶堆实现
    public int[] topKFrequent2(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数
        for(int num:nums){
            map.put(num,map.getOrDefault(num,0)+1);
        }
        //在优先队列中存储二元组(num,cnt),cnt表示元素值num在数组中的出现次数
        //出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(相当于小顶堆)
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1,pair2)->pair1[1]-pair2[1]);
        for(Map.Entry<Integer,Integer> entry:map.entrySet()){//小顶堆只需要维持k个元素有序
            if(pq.size()<k){//小顶堆元素个数小于k个时直接加
                pq.add(new int[]{entry.getKey(),entry.getValue()});
            }else{
                if(entry.getValue()>pq.peek()[1]){//当前元素出现次数大于小顶堆的根结点(这k个元素中出现次数最少的那个)
                    pq.poll();//弹出队头(小顶堆的根结点),即把堆里出现次数最少的那个删除,留下的就是出现次数多的了
                    pq.add(new int[]{entry.getKey(),entry.getValue()});
                }
            }
        }
        int[] ans = new int[k];
        for(int i=k-1;i>=0;i--){//依次弹出小顶堆,先弹出的是堆的根,出现次数少,后面弹出的出现次数多
            ans[i] = pq.poll()[0];
        }
        return ans;
    }
}

栈与队列

https://jiangzeshuo.github.io/2024/01/31/PartV_Stack/

Author

jzs

Posted on

2024-01-31

Updated on

2024-04-29

Licensed under

Comments

Follow

Links

Categories

Recents

Archives

Tags

Linux1
学习16
强化学习3
推荐系统5
数据结构6
深度学习2
算法11
计算机必备1
量子学习1
×