回溯2

93.复原IP地址

力扣题目链接

根据题目的意思是割3刀使所有部分是一个正确的ip地址所以除了判断有效的函数不同其他基本一致，但是终止条件式切3刀

class Solution {
private:
    vector<string> result;// 记录结果
    // startIndex: 搜索的起始位置，pointNum:添加逗点的数量
    void backtracking(string& s, int startIndex, int pointNum) {
        if (pointNum == 3) { // 逗点数量为3时，分隔结束
            // 判断第四段子字符串是否合法，如果合法就放进result中
            if (isValid(s, startIndex, s.size() - 1)) {
                result.push_back(s);
            }
            return;
        }
        for (int i = startIndex; i < s.size(); i++) {
            if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
                s.insert(s.begin() + i + 1 , '.');  // 在i的后面插入一个逗点
                pointNum++;
                backtracking(s, i + 2, pointNum);   // 插入逗点之后下一个子串的起始位置为i+2
                pointNum--;                         // 回溯
                s.erase(s.begin() + i + 1);         // 回溯删掉逗点
            } else break; // 不合法，直接结束本层循环
        }
    }
    // 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
    bool isValid(const string& s, int start, int end) {
        if (start > end) {
            return false;
        }
        if (s[start] == '0' && start != end) { // 0开头的数字不合法
                return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
                return false;
            }
            num = num * 10 + (s[i] - '0');
            if (num > 255) { // 如果大于255了不合法
                return false;
            }
        }
        return true;
    }
public:
    vector<string> restoreIpAddresses(string s) {
        result.clear();
        if (s.size() < 4 || s.size() > 12) return result; // 算是剪枝了
        backtracking(s, 0, 0);
        return result;
    }
};

• 时间复杂度: O(3^4)，IP地址最多包含4个数字，每个数字最多有3种可能的分割方式，则搜索树的最大深度为4，每个节点最多有3个子节点。

注意这个时间复杂度，这是递归方法的时间复杂度计算，就是针对于每个数字可能得情况我们进行遍历所以取得

78.子集

力扣题目链接

如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

你看对弈每一个节点都是子集并不是只存储最后的结果

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex) {
        result.push_back(path); // 收集子集，要放在终止添加的上面，否则会漏掉自己
        if (startIndex >= nums.size()) { // 终止条件可以不加
            return;
        }
        for (int i = startIndex; i < nums.size(); i++) {
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        result.clear();
        path.clear();
        backtracking(nums, 0);
        return result;
    }
};

90.子集II

力扣题目链接

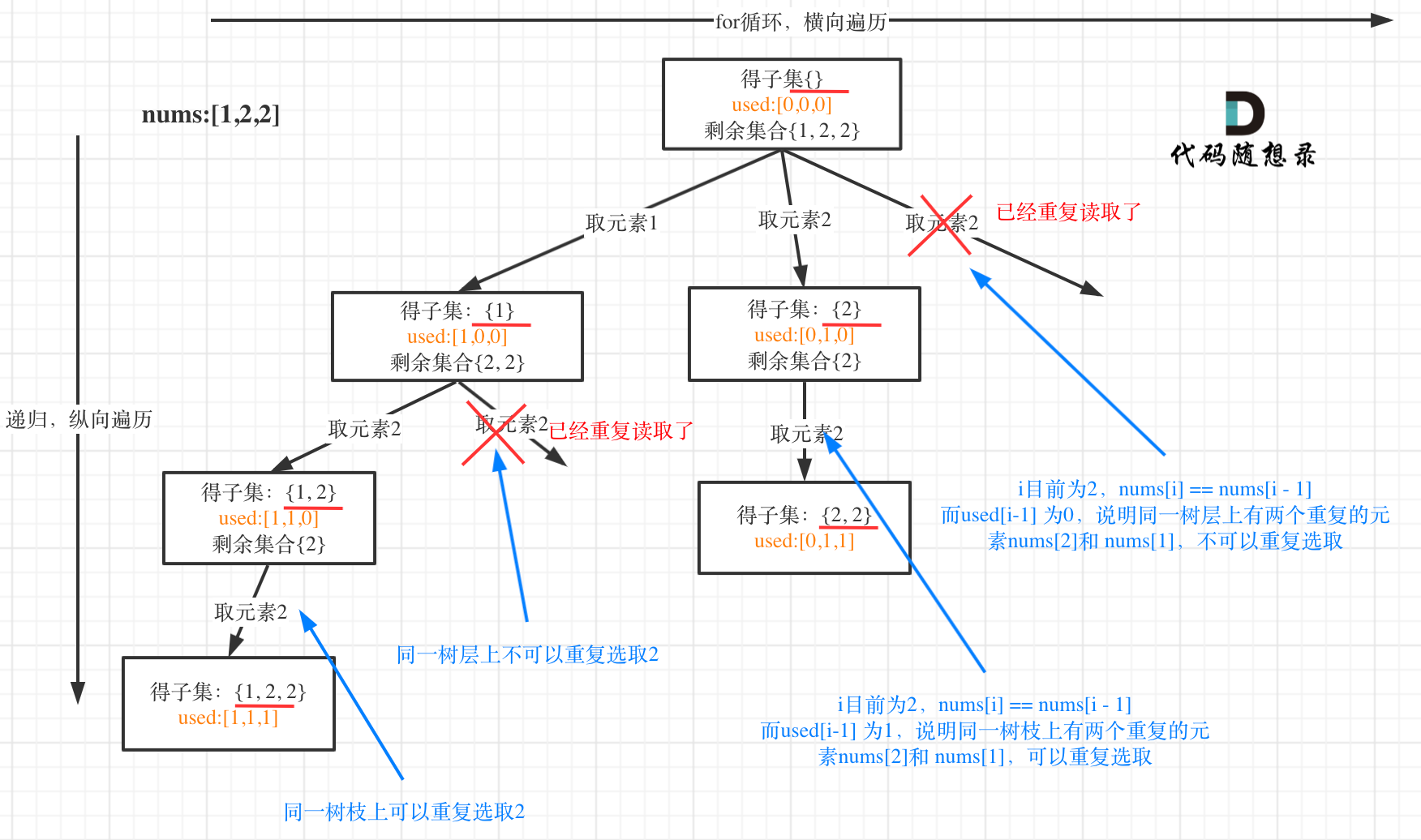
在78题的基础上利用use去重

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
        result.push_back(path);
        for (int i = startIndex; i < nums.size(); i++) {
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            // 而我们要对同一树层使用过的元素进行跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            path.push_back(nums[i]);
            used[i] = true;
            backtracking(nums, i + 1, used);
            used[i] = false;
            path.pop_back();
        }
    }

public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        result.clear();
        path.clear();
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end()); // 去重需要排序
        backtracking(nums, 0, used);
        return result;
    }
};

当然也可以使用set来去除重复数据。

491.递增子序列

力扣题目链接

这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。

这又是子集，又是去重，是不是不由自主的想起了刚刚讲过的90.子集II (opens new window)。

就是因为太像了，更要注意差别所在，要不就掉坑里了！

在90.子集II (opens new window)中我们是通过排序，再加一个标记数组来达到去重的目的。

而本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。

所以不能使用之前的去重逻辑！

// 版本一
class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex) {
        if (path.size() > 1) {
            result.push_back(path);
            // 注意这里不要加return，要取树上的节点
        }
        unordered_set<int> uset; // 使用set对本层元素进行去重
        for (int i = startIndex; i < nums.size(); i++) {
            if ((!path.empty() && nums[i] < path.back())
                    || uset.find(nums[i]) != uset.end()) {
                    continue;
            }
            uset.insert(nums[i]); // 记录这个元素在本层用过了，本层后面不能再用了
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        result.clear();
        path.clear();
        backtracking(nums, 0);
        return result;
    }
};

46.全排列

力扣题目链接

因为是排列问题所以也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方所以我们也就不需要使用startIndex

但是但排列问题需要一个used数组，标记已经选择的元素，如图橘黄色部分所示:

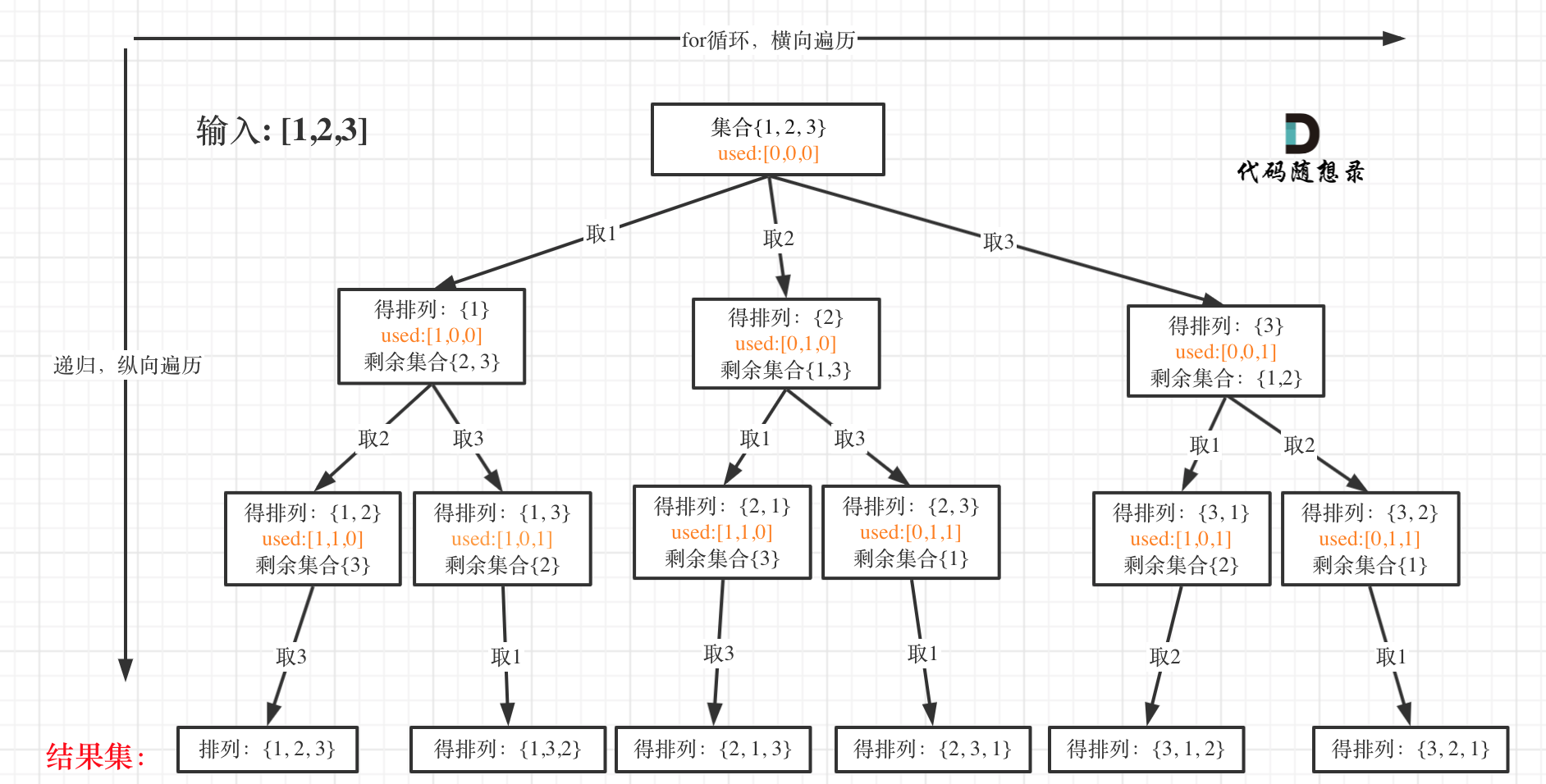
当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking (vector<int>& nums, vector<bool>& used) {
        // 此时说明找到了一组
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            if (used[i] == true) continue; // path里已经收录的元素，直接跳过
            used[i] = true;
            path.push_back(nums[i]);
            backtracking(nums, used);
            path.pop_back();
            used[i] = false;
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        result.clear();
        path.clear();
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};

47.全排列 II

力扣题目链接

这道题目和46.全排列 (opens new window)的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking (vector<int>& nums, vector<bool>& used) {
        // 此时说明找到了一组
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            // used[i - 1] == true，说明同一树枝nums[i - 1]使用过
            // used[i - 1] == false，说明同一树层nums[i - 1]使用过
            // 如果同一树层nums[i - 1]使用过则直接跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            if (used[i] == false) {
                used[i] = true;
                path.push_back(nums[i]);
                backtracking(nums, used);
                path.pop_back();
                used[i] = false;
            }
        }
    }
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        result.clear();
        path.clear();
        sort(nums.begin(), nums.end()); // 排序
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};