量子强化学习

背景

目前的研究主要集中在变分量子算法，之前的研究提出了利用变分量子算法来增强有监督、无监督和强化学习(RL)算法的建议。在这项工作中，我们采用一种基于深度q -学习算法的**参数化量子电路(PQC)**训练方法，该方法可用于解决离散和连续状态空间的RL任务。实验结果表明体系结构选择和超参数比模型中使用的参数数量对智能体的成功贡献更大。

经典强化学习

Q-learning关注的不是状态值函数，而是对密切相关的动作值函数Q(s, a)。

然后通过充分探索状态和动作空间。这为智能体提供了足够的信息来区分给定特定状态下的好行为和坏行为。来学习Q函数学习方法

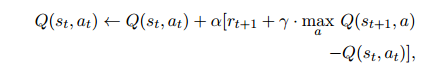
在Q-learning中，目标是近似实值最优q函数。在实际训练的过程中，模型不用知道每一个动作精确的Q，只用知道对于每一个状态动作，Q值的排序。也就是在当前状态做出哪个动作最好。

为了应对模型的复杂性，摒弃Q表的更新方式，提出了使用神经网络作为q函数逼近器，神经网络返回所有动作的Q值，然后通过上一次和这一次的q值估计的均方误差作为损失函数。

量子强化学习——量子Q学习

量子强化学习我们只将神经网络替换为量子强化学习网络。q-learning的其他方面比如greedy策略来确定代理的下一个动作，并通过重放来抽取样本以训练q 网络我们仍然采用。

量子比特（qubit）的理论基础通常通过布洛赫球（Bloch sphere）来说明。该模型封装了量子比特的状态及其所含信息[Gamel, 2016]。与经典计算机只能使用二进制 “0 “和 “1 “进行运算的情况不同，量子比特既可以存在于纯粹的 |0⟩ 或 |1⟩ 的纯态，也可以处于二者的叠加态，从而增加了成倍计算的可能性。

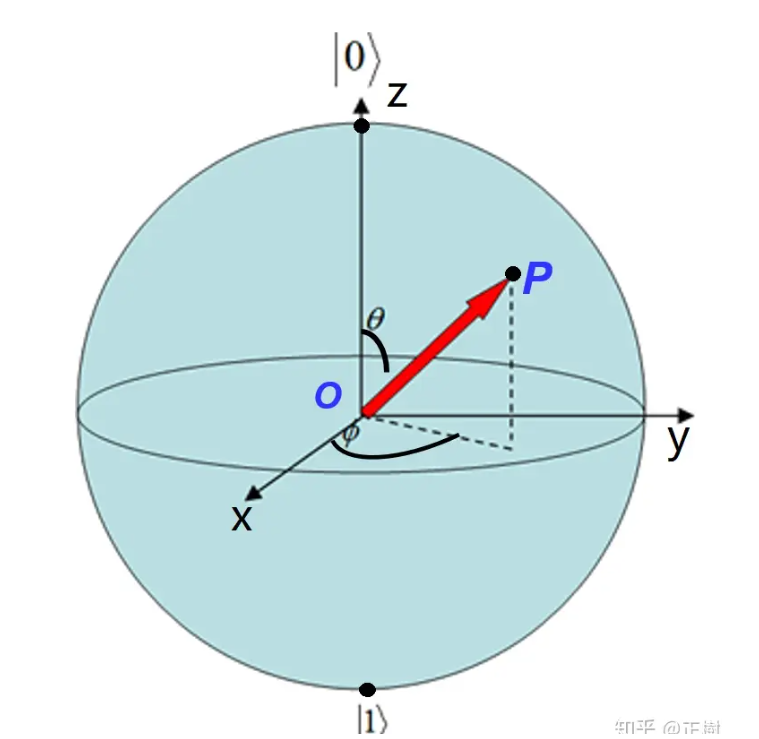
量子比特的旋转过程过程可以表示为

$|\psi\rangle=R_{z}(\theta_{z})R_{y}(\theta_{y})R_{x}(\theta_{x})|0\rangle,$

我们可以通过量子门电路Rx(θx)， Ry(θy)和Rz(θz)分别代表围绕Bloch球的x, y和z轴的 Pauli rotation泡利旋转操作。图中的θ就可以确认的参数。

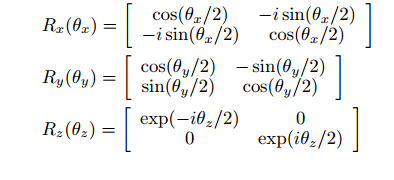
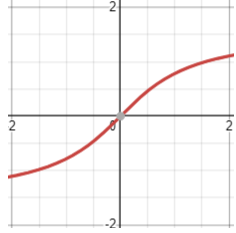
输入转换将获取的每个状态分别进行数值转换用一个qubit表示，

对于离散的状态我们可以使用纯态的0和1表示

对于连续的状态我们可以将它进行转换新的x代表量子比特

$x^{\prime}=\arctan(x)\in[-\pi/2,\pi/2]$

这些门对量子比特旋转角度和方向的影响是由它们的内部参数和唯一的操作规则决定的，所以我们可以将量子的旋转角度设置为参数，进行学习。

CZ门的连接，通过量子计算的CZ门可以让两个量子之间产生纠缠，增加量子之间的联系，增强信息交换的能力。 γ, α, β, δ 就是可以调整的参数。与神经网络的参数相对应。

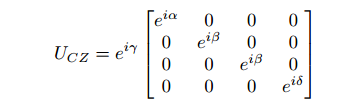
具体流程

1、信息编码

我们使用参数量子电路架构构建我们的QNN网络。针对特定的问题设置特定的QNN（量子神经网络）被特别设计以匹配系统环境。每个不同状态都分配了一个专用的量子比特用于信息编码。为了编码这些状态，QNN采用了在每个量子比特上使用Pauli-X门的旋转方法。

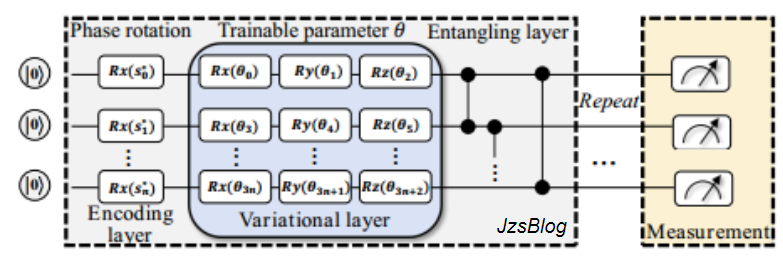
2、参数化旋转

每一层由每个量子位上沿Y和Z轴的参数化旋转和CZ门的组成。绿框对应于数据编码门，将数据编码为X旋转的参数。CZ门负责增加量子比特之间的联系的联系。在Pauli-X门处理完状态之后，每个量子比特然后通过变分层中的不同门进行调整。这些调整对量子比特的影响可以用前述方程1中提到的|ψ⟩表示。

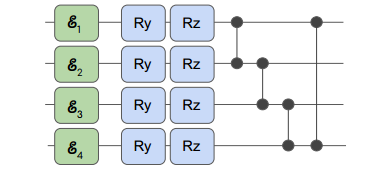
3、多层结构

为了进一步提高电路的表现力，数据编码可以以两种方式重复:通过增加量子位的数量并在其上复制数据编码来并行地重复，或者以交替的方式与电路的变分层顺序重复（数据重上传）。使用数据重新加载，每层重复绘制整个电路图，只重复没有初始X旋转的变分部分。

4、模型输出

通过不断地增加多层结构，最后设置相应的CZ门设置输出输出控制动作。

$|\Phi_{\mathrm{out}}\rangle=\mathrm{CZ}(|\phi_{1}^{\prime\prime}\rangle,\mathrm{CZ}(|\phi_{2}^{\prime\prime}\rangle,\mathrm{CZ}(\ldots\mathrm{CZ}(|\phi_{6}^{\prime\prime}\rangle,|\phi_{7}^{\prime\prime}\rangle)\ldots)))$