推荐系统-用户数据分析
它基于用户之间的相似性或项目之间的相似性来进行推荐,基于用户行为分析的推荐算法是个性化推荐系统的重要算法。顾名思义,协同过滤就是指用户可以齐心协力,通过不断地和网站互动,使自己的推荐列表能够不断过滤掉自己不感兴趣的物品,从而越来越满足自己的需求。
用户行为数据
简介
很多的用户行为数据都会以日志的形式 ,但是一般使用的都是会话日志( session log) 其中每个会话表示一次用户行为和对应的服务。比如,在搜索引擎和搜索广告系统中,服务会为每次查询生成一个展示日志( impression log),其中记录了查询和返回结果。如果用户点击了某个结果,这个点击信息会被服务器截获并存储在点击日志( click log)中 。得到的会话日志中每个消息是一个用户提交的查询、得到的结果以及点击。
分类
用户行为一般分为显性反馈行为( explicit feedback)和隐性反馈行为( implicit feedback)。 比如喜欢/不喜欢,购买差评都是显性反馈行为 。 用户浏览一个物品 ,用户点击界面。显性反馈行为和隐性反馈行为的比较如下。

用户行为分析
长尾效应
指那些原来不受到重视的销量小但种类多的产品或服务由于总量巨大,累积起来的总收益超过主流产品的现象。 维基
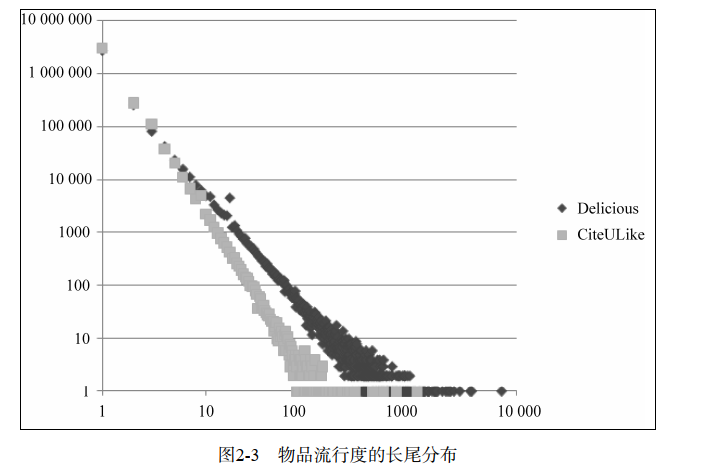
下图是Delicious和CiteULike数据集中物品流行度的分布曲线。横坐标是物品的流行度K,纵坐标是流行度为K的物品的总数。这里,物品的流行度指对物品产生过行为的用户总数。 完美的展现了展示了长尾效应。
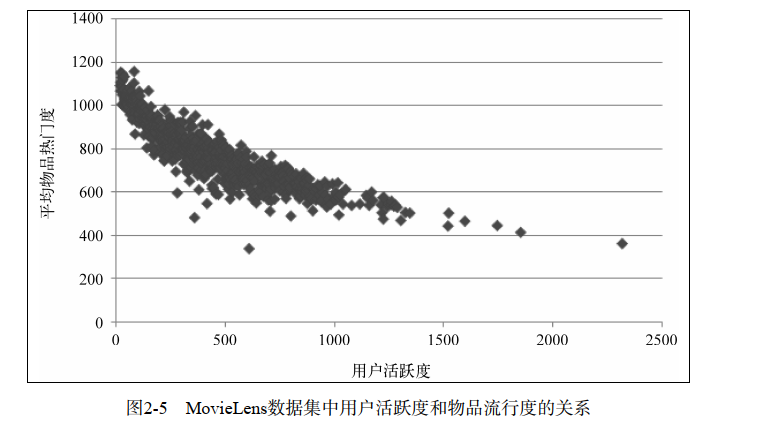
用户活跃度和物品流行度的关系
一般认为,新用户倾向于浏览热门的物品,因为他们对网站还不熟悉,只能点击首页的热门物品,而老用户会逐渐开始浏览冷门的物品。图2-5展示了MovieLens数据集中用户活跃度和物品流行度之间的关系,其中横坐标是用户活跃度,纵坐标是具有某个活跃度的所有用户评过分的物品的平均流行度。这表明用户越活跃,越倾向于浏览冷门的物品。 所以为了留住用户,我们就需要进行个性化的推荐。
实验准备
本章采用GroupLens提供的MovieLens数据集介绍和评测各种算法。 MovieLens数据集有3个不同的版本,本章选用中等大小的数据集,着重研究隐反馈数据集中的TopN推荐问题 。
测评指标:
精度:通过准确率/召回率评测推荐算法的精度
覆盖率:反映了推荐算法发掘长尾的能力
新颖度 :如果推荐出的物品都很热门,说明推荐的新颖度较低,否则说明推荐结果比较新颖。
基于邻域的算法
基于邻域的算法分为两大类,一类是基于用户的协同过滤算法,另一类是基于物品的协同过滤算法。
基于用户的协同过滤算法
在一个在线个性化推荐系统中,当一个用户A需要个性化推荐时,可以先找到和他有相似兴趣的其他用户,然后把那些用户喜欢的、而用户A没有听说过的物品推荐给A。这种方法称为基于用户的协同过滤算法。
主要包括如下两个步骤
- 找到和目标用户兴趣相似的用户集合。
- 找到这个集合中的用户喜欢的,且目标用户没有听说过的物品推荐给目标用户
步骤1:
兴趣相似度:
$w_{uv}=\frac{\left|N(u)\cap N(v)\right|}{\left|N(u)\cup N(v)\right|}$
余弦兴趣相似度:
$w_{uv}=\frac{\left|N(u)\cap N(v)\right|}{\sqrt{\left|N(u)\right|\left|N(v)\right|}}$
举例

一个小技巧:在计算相似度时当用每个用户与每个用户计算相似度时间复杂度是O(|U|*|U|) U是用户个数,但是很多的用户并没有相似的交集所以
我们可以进行物品到用户的倒排表,对于每个物品都保存对该物品产生过行为的用户列表 。从而,可以扫描倒排表中每个物品对应的用户列表,将用户列表中的两两用户对应的C[u][v]加1,最终就可以得到所有用户之间不为0的。
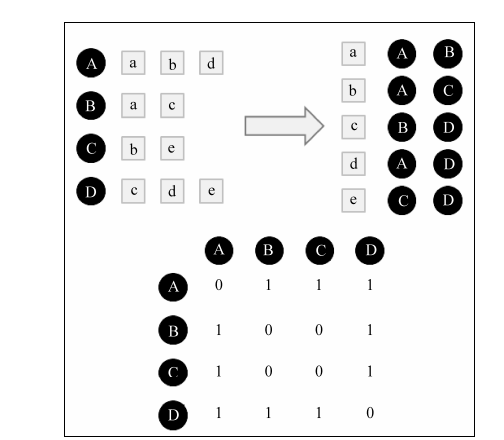
步骤2:
得到用户之间的兴趣相似度后, 可以通过UserCF算法中用户u对物品i的感兴趣程度 :
$p(u,i)=\sum_{v\in S(u,K)\cap N(i)}w_{u\nu}r_{vi}$
S(u, K)包含和用户u兴趣最接近的K个用户, N(i)是对物品i有过行为的用户集合,所以v是即对物品i感兴趣又与用户u有一定相似度的用户。${w_{uv}}$是用户u和用户v的兴趣相似度,${r_{vi}}$代表用户v对物品i的兴趣
结果分析
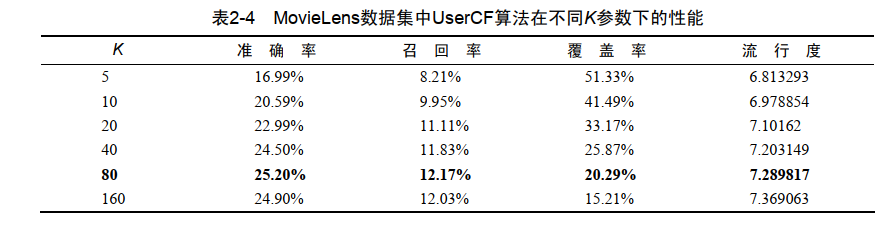
UserCF的准确率和召回率相对MostPopular算法提高了将近1倍。同时, UserCF的覆盖率远远高于MostPopular,推荐结果相对MostPopular不太热门。
并且K值影响着流行度可以看到,随着额K越大则UserCF推荐结果就越热门。这是因为K决定了UserCF在给你做推荐时参考多少和你兴趣相似的其他用户的兴趣,那么如果K越大,参考的人越多,结果就越来越趋近于全局热门的物品。 K越大则UserCF推荐结果的覆盖率越低。覆盖率的降低是因为流行度的增加,随着流行度增加, UserCF越来越倾向于推荐热门的物品, 从而对长尾物品的推荐越来越少,因此造成了覆盖率的降低 。

改进User-IIF
两个用户对冷门物品采取过同样的行为更能说明他们兴趣的相似度。 对于热门商品(比如新华字典)两人都购买但是并不能显示他们的相似度
所以改进相似度计算公式:
$w_{uv}=\frac{\sum_{i\in N(u)\cap N(v)}\frac{1}{\log1+\left|N(i)\right|}}{\sqrt{\left|N(u)\right|\left|N(v)\right|}}$
对于物品i如果他的交互用户很多,那么分子部分就很很小,这样就是对热门商品的惩罚。
效果:经过对热门商品的惩罚,可以看到覆盖率的提升和流行度的下降证明推荐系统在变好。

基于物品的协同过滤算法
基于物品的协同过滤算法(简称ItemCF)给用户推荐那些和他们之前喜欢的物品相似的物品 。不过, ItemCF算法并不利用物品的内容属性计算物品之间的相似度,它主要通过分析用户的行为记录计算物品之间的相似度。
主要包括如下两个步骤
- 计算物品之间的相似度。
- 根据物品的相似度和用户的历史行为给用户生成推荐列表。
步骤1:
$w_{ij}=\frac{\left|N(i)\cap N(j)\right|}{\left|N(i)\right|}$
这里,分母|N(i)|是喜欢物品i的用户数,而分子 N i N j ( ) ( ) 是同时喜欢物品i和物品j的用户数。因此,上述公式可以理解为喜欢物品i的用户中有多少比例的用户也喜欢物品j。
为了避免推荐出热门的物品,可以用下面的公式:
$w_{ij}=\frac{\left|N(i)\cap N(j)\right|}{\sqrt{\left|N(i)\right|\left|N(j)\right|}}$
如果物品j是人们物品那么会增大分母进而对权重进行惩罚。
Q:为什么计算谁喜欢这个物品可以代表物品之间的相似度。
A:在协同过滤中两个物品产生相似度是因为它们共同被很多用户喜欢,也就是说每个用户都可以通过他们的历史兴趣列表给物品“贡献”相似度。这里面蕴涵着一个假设,就是每个用户的兴趣都局限在某几个方面,因此如果两个物品属于一个用户的兴趣列表,那么这两个物品可能就属于有限的几个领域,而如果两个物品属于很多用户的兴趣列表,那么它们就可能属于同一个领域,因而有很大的相似度。
步骤2:
在得到物品之间的相似度后, ItemCF通过如下公式计算用户u对一个物品j的兴趣:
$p_{uj}=\sum_{i\in N(u)\cap S(j,K)}w_{ji}r_{ui}$
这里N(u)是用户喜欢的物品的集合, S(j,K)是和物品j最相似的K个物品的集合, 所以i属于用户u喜欢的物品并且还和i有相关性的物品。${w_{ij}}$是物品j和i的相似度,${r_{ui}}$是用户u对物品i的兴趣。 该公式的含义是,和用户历史上感兴趣的物品越相似的物品,越有可能在用户的推荐列表中获得比较高的排名。
例子:
用户喜欢《 C++ Primer中文版》和《编程之美》两本书。然后ItemCF会为这两本书分别找出和它们最相似的3本书,然后根据公式的定义计算用户对每本书的感兴趣程度。比如, ItemCF给用户推荐《算法导论》,是因为这本书和《 C++ Primer中文版》相似,相似度为0.4,而且这本书也和《编程之美》相似,相似度是0.5。考虑到用户对《 C++ Primer中文版》的兴趣度是1.3,对《编程之美》的兴趣度是0.9,那么用户对《算法导论》的兴趣度就是1.3 (${r_{ui}}$)× 0.4 ${w_{ij}}$+ 0.9× 0.5 = 0.97
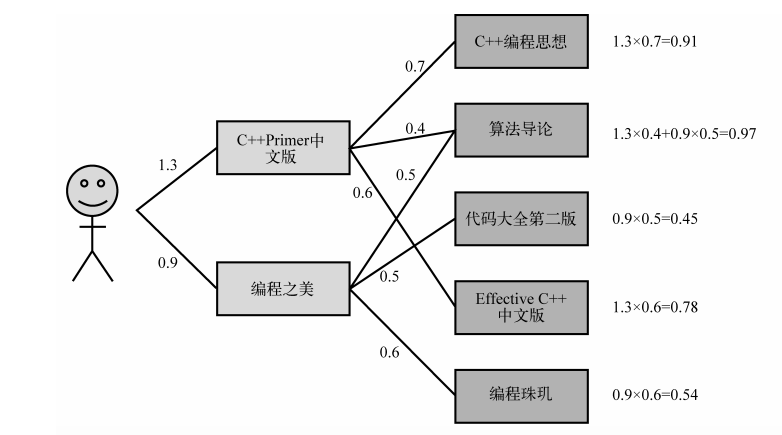
结果:
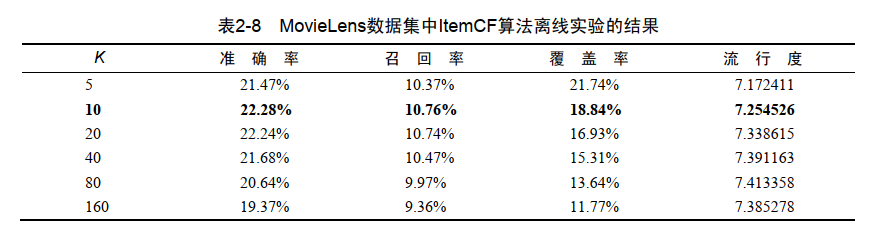
改进ItemCF-IUF
用户活跃度对数的倒数的参数,他也认为活跃用户对物品相似度的贡献应该小于不活跃的用户。
$w_{ij}=\frac{\sum_{u\in N(i)\cap N(j)}\frac{1}{\log1+\left|N(u)\right|}}{\sqrt{\left|N(i)\right|\left|N(j)\right|}}$
N(i)N(j)是同时喜欢物品i和物品j的用户 ,N(u)是代表用户u喜欢的物品数目,这样可以减少异常活跃用户对于相关性的影响
ItemCF-IUF在准确率和召回率两个指标上和ItemCF相近,但ItemCF-IUF明显提高了推荐结果的覆盖率,降低了推荐结果的流行度

改进ItemCF-Norm
假设物品分为两类——A和B, A类物品之间的相似度为0.5, B类物品之间的相似度为0.6,而A类物品和B类物品之间的相似度是0.2。在这种情况下,如果一个用户喜欢了5个A类物品和5个B类物品,用ItemCF给他进行推荐,推荐的就都是B类物品,因为B类物品之间的相似度大。但如果归一化之后, A类物品之间的相似度变成了1, B类物品之间的相似度也是1,那么这种情况下,用户如果喜欢5个A类物品和5个B类物品,那么他的推荐列表中A类物品和B类物品的数目也应该是大致相等的。
$w_{ij}^{‘}=\frac{w_{ij}}{\max_{j}w_{ij}}$

UserCF和ItemCF的综合比较

为什么原始ItemCF算法的覆盖率和新颖度都不高
如果j非常热门,那么上面公式的分子$\begin{vmatrix}N(i)\cap N(j)\end{vmatrix}$就会越来越接近 $\begin{vmatrix}N(i)\end{vmatrix}$。尽管上面的公式分母已经考虑到了j的流行度,但在实际应用中,热门的j仍然会获得比较大的相似度。
解决方案我们可以在分母上加大对热门物品的惩罚, 通过提高α,就可以惩罚热门的j。
$w_{ij}=\frac{\left|N(i)\cap N(j)\right|}{\left|N(i)\right|^{1-\alpha}\left|N(j)\right|^\alpha}$
隐语义模型
LFM( latent factor model)隐语义模型 用于找到文本的隐含语义
如果要推荐一本书处理上述的user-CF和item-CF还有一种方法,可以对书和物品的兴趣进行分类。对于某个用户,首先得到他的兴趣分类,然后从分类中挑选他可能喜欢的物品。
LFM通过如下公式计算用户u对物品i的兴趣: 这个公式中${p_{u,k}}$, 和${q_{i,k}}$ 是模型的参数,其中${p_{u,k}}$,度量了用户u的兴趣和第k个隐类的关系,而${q_{i,k}}$ , 度量了第k个隐类和物品i之间的关系。
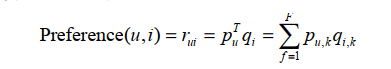
LFM在隐性反馈数据 如何生成负样本
对于一个用户,从他没有过行为的物品中均匀采样出一些物品作为负样本。
采样原则
- 对每个用户,要保证正负样本的平衡(数目相似)。
- 对每个用户采样负样本时,要选取那些很热门,而用户却没有行为的物品。
损失函数是均方误差,优化方法随机梯度下降法 来对训练集进行训练。
结果
表中展示了4个隐类中排名最高( qik最大)的一些电影。结果表明,每一类的电影都是合理的,都代表了一类用户喜欢看的电影。从而说明LFM确实可以实现通过用户行为将物品聚类的功能。

LFM和基于邻域的方法的比较
- 理论基础 LFM具有比较好的理论基础,它是一种学习方法,通过优化一个设定的指标建立最优的模型。基于邻域的方法更多的是一种基于统计的方法,并没有学习过程。
- 离线计算的空间复杂度 基于邻域的方法需要维护一张离线的相关表。在离线计算相关表的过程中,如果用户/物品数很多,将会占据很大的内存。假设有M个用户和N个物品,在计算相关表的过程中,我们可能会获得一张比较稠密的临时相关表(尽管最终我们对每个物品只保留K个最相关的物品,但在中间计算过程中稠密的相关表是不可避免的),那么假设是用户相关表,则需要O(MM)的空间,而对于物品相关表,则需要O(NN)的空间。而LFM在建模过程中,如果是F个隐类,那么它需要的存储空间是O(F*(M+N)),这在M和N很大时可以很好地节省离线计算的内存。在Netflix Prize中,因为用户数很庞大( 40多万),很少有人使用UserCF算法(据说需要30 GB左右的内存),而LFM由于大量节省了训练过程中的内存(只需要4 GB),从而成为Netflix Prize中最流行的算法。
- 在线实时推荐 UserCF和ItemCF在线服务算法需要将相关表缓存在内存中,然后可以在线进行实时的预测。以ItemCF算法为例,一旦用户喜欢了新的物品,就可以通过查询内存中的相关表将和该物品相似的其他物品推荐给用户。因此,一旦用户有了新的行为,而且该行为被实时地记录到后台的数据库系统中,他的推荐列表就会发生变化。 而从LFM的预测公式可以看到, LFM在给用户生成推荐列表时,需要计算用户对所有物品的兴趣权重,然后排名,返回权重最大的N个物品。那么,在物品数很多时,这一过程的时间复杂度非常高,可达O(MNF)。因此, LFM不太适合用于物品数非常庞大的系统,如果要用,我们也需要一个比较快的算法给用户先计算一个比较小的候选列表,然后再用LFM重新排名。另一方面, LFM在生成一个用户推荐列表时速度太慢,因此不能在线实时计算,而需要离线将所有用户的推荐结果事先计算好存储在数据库中。因此, LFM不能进行在线实时推荐,也就是说,当用户有了新的行为后,他的推荐列表不会发生变化。
- 推荐解释 ItemCF算法支持很好的推荐解释,它可以利用用户的历史行为解释推荐结果。但LFM无法提供这样的解释,它计算出的隐类虽然在语义上确实代表了一类兴趣和物品,却很难用自然语言描述并生成解释展现给用户。
基于图的模型
将用户行为表示为二分图模型后, 下面的任务就是在二分图上给用户进行个性化推荐。如果将个性化推荐算法放到二分图模型上,那么给用户u推荐物品的任务就可以转化为度量用户顶点vu和与vu没有边直接相连的物品节点在图上的相关性
度量图中两个顶点之间相关性的方法很多,但一般来说图中顶点的相关性主要取决于下面:
- 两个顶点之间的路径数;
- 两个顶点之间路径的长度;
- 两个顶点之间的路径经过的顶点
而相关性高的一对顶点一般具有如下特征:
- 两个顶点之间有很多路径相连;
- 连接两个顶点之间的路径长度都比较短;
- 连接两个顶点之间的路径不会经过出度比较大的顶点。
举例
举一个简单的例子,如图2-19所示,用户A和物品c、 e没有边相连,但是用户A和物品c有两条长度为3的路径相连,用户A和物品e有两条长度为3的路径相连。那么,顶点A与e之间的相关性要高于顶点A与c,因而物品e在用户A的推荐列表中应该排在物品c之前,因为顶点A与e之间有两条路径——( A, b, C, e)和( A, d, D, e)。其中, ( A, b, C, e)路径经过的顶点的出度为( 3, 2, 2, 2),而( A, d, D, e)路径经过的顶点的出度为( 3, 2, 3, 2)。因此, ( A, d, D, e)经过了一个出度比较大的顶点D,所以( A, d, D, e)对顶点A与e之间相关性的贡献要小于( A, b, C, e)
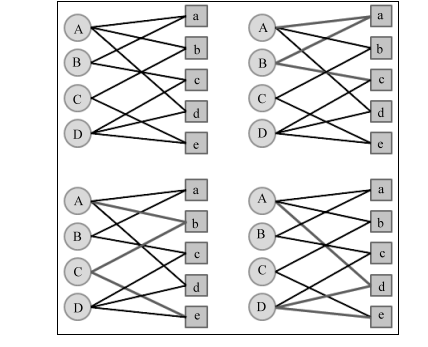
假设要给用户u进行个性化推荐,可以从用户u对应的节点vu开始在用户物品二分图上进行随机游走。游走到任何一个节点时,首先按照概率α 决定是继续游走,还是停止这次游走并从vu节点开始重新游走。如果决定继续游走,那么就从当前节点指向的节点中按照均匀分布随机选择一个节点作为游走下次经过的节点。
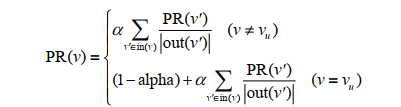
虽然PersonalRank算法可以通过随机游走进行比较好的理论解释,但该算法在时间复杂度上有明显的缺点。因为在为每个用户进行推荐时,都需要在整个用户物品二分图上进行迭代,直到整个图上的每个顶点的PR值收敛。这一过程的时间复杂度非常高,不仅无法在线提供实时推荐,甚至离线生成推荐结果也很耗时。